One of the most beautiful things about the theory of computation is, in my opinion, how you start from something as simple and intuitive as a finite-state machine and then – with a few more bells and whistles – end up with something as complex and powerful as a Turing machine. When someone mockingly says that machine learning or deep learning is just regression, and that often implies merely linear regression, they are missing a similar jump in complexity as the one from finite-state to Turing machines.
In this post, we will look at rectifier networks: one of the simplest but yet very expressive type of artificial neural network. A rectifier network is made of Rectified Linear Units, or ReLUs, and each ReLU defines a linear function on its inputs that is then composed with a non-linear function that takes the maximum between 0 and that linear function. If the output is positive, we say that the input has activated the ReLU. At the microscopic level, one would be correct to think that adjusting the coefficients of the linear function associated with each ReLU during training is akin to linear regression (and at the same time this person could be puzzled that the negative outputs produced when a ReLU is not activated are thrown away).
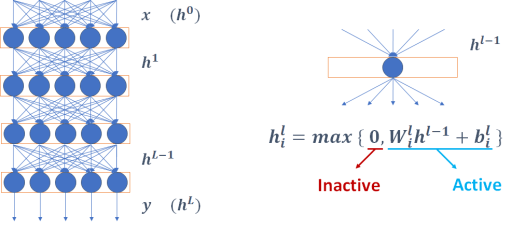
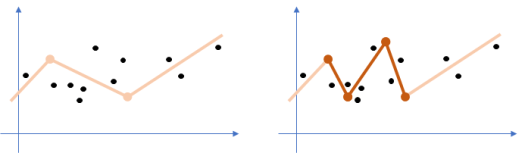
However, what happens at the macroscopic level when many ReLUs are put together is very different. If we were to combine units defining just linear functions, we would get a single linear function as a result. But as we turn negative outputs into zeroes, we obtain different linear functions for different inputs, and consequently the neural network models a piecewise linear function instead. That alone implies a big jump in complexity. Intuitively, we may guess that having a function with more pieces would make it easier to fit the training data. According to our work so far, that seems correct.
Here is what we found out in prior work published at ICML 2018:
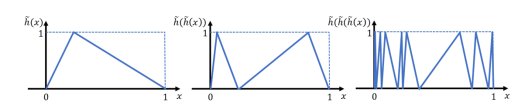
- The maximum number of these pieces, which are also called linear regions, may grow exponentially on the depth of the neural network. By extending prior results along the same lines, where a zigzagging function is modeled with the network, we have shown that a neural network with one-dimensional input and L layers having n ReLUs each can define a maximum of (n+1)^L linear regions instead of n^L.
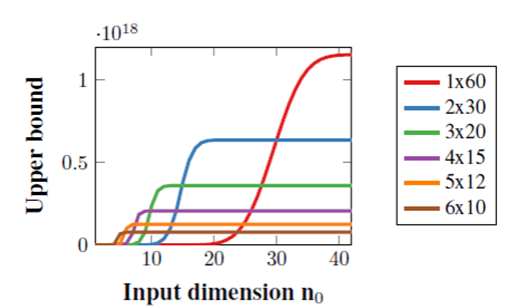
- Surprisingly, however, too much depth may also hurt the number of linear regions. If we distribute 60 ReLUs uniformly among 1 to 6 layers, the best upper bound on the number of linear regions will be attained by different depths depending on the size of input. Because this upper bound is tight for a single layer, that implies that a shallow network may define more linear regions if the input is sufficiently large.
- If no layer in a small neural network trained on the MNIST dataset is too narrow (3 units or less), we found that the accuracy of the network relates to the number of linear regions. However, it takes a long time to count linear regions even in small neural networks (for example, sometimes almost a week with just 32 ReLUs).
In the paper that we are presenting at AAAI 2020, we describe a fast estimate on the number of linear regions (i.e., pieces of the piecewise linear function) that could be used to measure larger neural networks. We can map inputs to outputs of a rectifier network using a mixed-integer linear programming (MILP) formulation that also includes binary (0-1) variables denoting which units are activated or not by different values for the input. Every linear region corresponds to a different vector of binary values denoting which units are activated, so we just need to count all binary vectors that are feasible. The formulation below connects inputs to the output of a single ReLU.

What makes counting so slow – besides the fact that the number of linear regions grows very fast with the size of the neural network – is that there is little research on counting solutions of MILP formulations. And that is justifiable: research and development in operations research (OR) methodologies such as MILP are focused on finding a good (and preferably optimal) solution as fast as possible. Meanwhile, counting solutions of propositional satisfiability (SAT) formulas, which involve only Boolean variables, is a widely explored topic back in artificial intelligence (AI). For example, we can test multiple times how many additional clauses would it take to make a SAT formula unsatisfiable and then draw conclusions on the total number of solutions based on that. There is no reason why the same methods could not be applied to count solutions on binary variables in MILP formulations.

In other words, we started with an AI problem of counting linear regions, moved to an OR problem of counting solutions of an MILP formulation, and came back to AI to use approximate model counting methods that are typically applied to SAT formulas. However, there is something special about MILP solvers that can make approximate counting more efficient: callback functions. Most of the SAT literature is based on the assumption that testing the satisfiability of a formula with every set of additional clauses requires solving that formula from scratch. With a lazy cut callback in an MILP solver, we can add more constraints as soon as a new solution is found. Consequently, we reduce the number of times that we have to prove that a formulation is infeasible, which is computationally very expensive.
By adding random parity (XOR) constraints involving a few binary variables to iteratively restrict the number of solutions of the MILP formulation, we obtained probabilistic lower bounds on the number of linear regions that are very similar in shape to the actual figures. On the left of the figure below, we are analyzing 10 networks trained on the MNIST dataset for every possible combination of 22 ReLUs distributed in two hidden layers followed by 10 ReLUs of output. The black and red curves on top are upper bounds, the black dots are averages of the exact number of linear regions, and the line charts below are lower bounds with probability 95%. On the right of the figure below, we see that the probabilistic lower bounds are orders of magnitude faster to calculate if the actual number of linear regions is large (at least 1 million each).
If you are curious about our next steps, take a look at our upcoming CPAIOR 2020 paper, where we look at this topic from a different perspective by asking the following: do we need a trained neural network to be as wide or as deep as it is to do what it does? If a network is trained with L1 regularization, the answer is probably not! We use MILP to identify units that can be removed or merged in a neural network without affecting the outputs that are produced. In other words, we obtain a lossless compression.
Where to find our work at AAAI 2020:
- Spotlight Presentation: Sunday, 11:15 – 12:30, Clinton (Technical Session 9: Constraint Satisfaction and Optimization)
- Poster Presentation: Sunday, 7:30 – 9:30, Americas Halls I/II
Links to our papers:
- Bounding and Counting Linear Regions of Deep Neural Networks (ICML 2018)
- Empirical Bounds on Linear Regions of Deep Rectifier Networks (AAAI 2020)
- Lossless Compression of Deep Neural Networks (CPAIOR 2020)
All papers are joint work with Srikumar Ramalingam. Christian Tjandraatmadja is a co-author in the ICML 2018 paper. Abhinav Kumar is a co-author in the CPAIOR 2020 paper.

Hi Thiago, great post. I think I am missing something fundamental here. Are you trying to find (or estimate in a fast way) how many regions a neural network has? Is the number of regions a measure of quality?
Yes for both questions.